概率论/数理统计里，k阶矩实际上就是想表示k个「维度」下的move to average（移动到平均位置）这么件事儿，也就是把一列随机变量的(probability) mass之类的东西集中到一点，然后等效为「一个（k阶的）瞬间」，将所有的（一到无穷阶）「瞬间」集合到一起，可以完整描述这列随机变量。和物理里moving power的想法如出一辙，所以聪明的老人家用了moment（矩）这个词。

于是，不论是概率论/数理统计中，还是物理中的矩，在数学里可以被抽象成了同一类泛函： $\int x^k f(x) dx$ 。

具体而言：

零阶矩，（概率）质量的总和。

一阶原点矩，即均值，也是大众理解的那个「平均」——衡量数据的平均水平。

二阶中心距，方差，衡量数据的离散/集中程度，也就是数据的「平均程度」。（这个表述不是很好，请大家脑补体会一下我的真实意思……）

二阶原点矩， $\mathbb{E}X^2$ ，衡量数据被「移动至平均位置」需要的「平均能量」。相当于物理中的惯性矩。

三阶中心矩，偏度，衡量偏离中心的点的位置情况，也就是偏离中心的点的平均水平（正负、大小）。放到分布图像上看，就是均值和中位数之间的距离，也就是数据分布的对称性——对称分布偏度为零。

四阶中心矩，峰度，俗称「方差的方差」，衡量偏离中心的点的密集程度。是俗话说的「尖峰厚尾」的理论基础。

以此类推。

但四阶以上的矩在实际数据使用中，计算繁杂且几乎没有太多必要计算，故很少讨论。

总之是蛮富有想象力的一个概念，对物理（刚体力学）的矩的解释也同样make sense。说白了就一坨点乘、一个内积。

哈哈哈哈哈哈嗝。

课后思考题：条件期望的物理解释。

题外话：矩和鞅是我觉得概率/统计里，无论中英文都定义得最好、最可爱的两个专有名词了> <

其实我更想知道norm的物理解释。

学过物理的朋友给我科普一下呗~

编辑于 2019-08-13

矩的理解

物理意义

数学中矩的概念来自物理学。在物理学中，矩是表示距离和物理量乘积的物理量，表征物体的空间分布。由其定义，矩通常需要一个参考点（基点或参考系）来定义距离。如力和参考点距离乘积得到的力矩（或扭矩），原则上任何物理量和距离相乘都会产生力矩，质量，电荷分布等。

单个点的力矩：

$\mu_n=r^n Q$

多个点则是积分的空间密度

$\mu_n=\int r^n \rho(r) \mathrm{d}r$

如果点表示质量，则第零矩是总质量，一阶矩是重心，二阶矩是转动惯量

$I=r^2 m$

$\sum_i r_i^2 m_i$

还有一个多极矩的概念，设计到极坐标系和球面坐标，就不多说了，读者可以自己参考这个链接link

数学意义

矩是物体形状识别的重要参数指标。在统计学中，矩表征随机量的分布。如一个“二阶矩”在一维上可测量其“宽度”，在更高阶的维度上由于其使用于橢球的空间分布，我们还可以对点的云结构进行测量和描述。其他矩用来描述诸如与均值的偏差分布情况（偏态），或峰值的分布情况（峰态）

定义在实数域的实函数相对于值c的n阶矩为：

$\mu '_n=\int_{-\infty}^{\infty} (x-c)^n \,f(x)\,dx$

如果点表示概率密度，则第零阶矩表示总概率（即1）,1,2,3阶矩依次为以下三项。数学中的概念与物理学中矩的概念密切相关。

期望
随机变量的期望定义为其一阶原点矩：

$E(x)=\int_{-\infty}^{\infty} x\,f(x)\,dx$

在方差等定义中，期望也成为随机变量的“中心”。
显然，任何随机变量的一阶中心据为0。对于以下二阶及更高阶的矩，通常使用中心矩（围绕平均值c的矩，均值是一阶矩），而不是原点矩，因为中心矩能更清楚的体现关于分布形状的信息。

方差
随机变量的方差定义为其二阶中心矩：

$Var(x)=\int_{-\infty}^{\infty} [x-E(x)]^2 \,f(x)\,dx$

归一化矩
归一化n阶中心矩或者说标准矩，是n阶中心矩除以标准差 σnσn,归一化n阶中心矩为：
$x=\frac{E[(x-\mu)^n]}{\sigma^n}$
这些归一化矩是无量纲值，表示独立于任何尺度的线性变化的分布。举个栗子，对于电信号，一阶矩是其DC(直流)电平，二阶矩与平均功率成比例。

偏态

随机变量的偏态（衡量分布不对称性）定义为其三阶中心矩: $S(x)=\int _{-\infty }^{\infty }[x-E(x)]^{3}\,f(x)\,dx$

需要注意，任何对称分布偏态为0，归一化三阶矩被成为偏斜度，向左偏斜（分布尾部在左侧较长）具有负偏度（失效率数据常向左偏斜，如极少量的灯泡会立即烧坏），向右偏斜分布（分布尾部在右侧较长）具有正偏度（工资数据往往以这种方式偏斜，大多数人所得工资较少）。

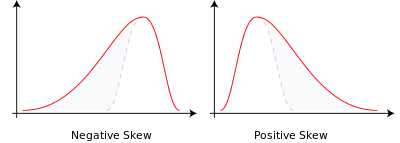
峰度

一般随机变量的峰度定义为其四阶中心矩与方差平方的比值再减3，减3是为了让正态分布峰度为0，这也被称为超值峰度：

$K(x)=\frac{\int _{-\infty }^{\infty }[x-E(x)]^{4}\,f(x)\,dx}{\sigma^2}-3$

峰度表示分布的波峰和尾部与正态分布的区别，峰度有助于初步了解数据分布的一般特征。

完全符合正态分布的数据峰度值为0,且正态分布曲线被称为基线。如果样本峰度显著偏离0，就可判断此数据不是正态分布

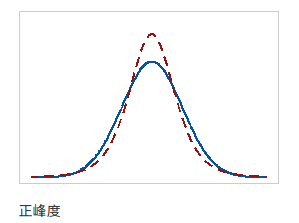
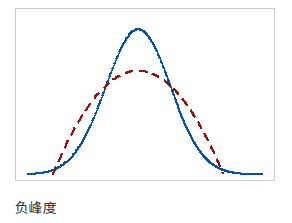
混合矩

混合矩是多个变量的矩，比如协方差，协偏度，协峰度。虽然协方差只有一个，但协偏度和协峰度存在多个。

中心转换

由于： $(x-b)^n=(x-a+a-b)^n=\sum\limits_{i=0}^n \left( \begin{array}{c} c\\r \end{array} \right) (x-a)^i (a-b)^{n-i}$

所以： $E[(x-b)^n]= \sum\limits_{i=0}^n \left( \begin{array}{c} c\\r \end{array} \right) E[(x-a)^i](a-b)^{n-i}$

累加性

当x和y是独立变量时，

$m_1(x+y)=m_1(x)+m_1(y) \\ Var(x+y)=Var(x)+Var(y)\\\mu_3(x+y)=\mu_3(x)+\mu_3(y)$

样本矩

矩常常通过样本矩来估计，这种方法不需要先估计其概率分布。

$\mu '_{n}\approx {\frac {1}{N}}\sum _{i=1}^{N}X_{i}^{n}$

对于任何样本大小，原始样本矩的期望值等于群体的k阶矩（若存在）。

图像意义

在图像处理，计算机视觉和相关领域中，一个图像矩是图像像素强度的某个特定加权平均（矩），或者是这样的矩的函数，通常选择具有一些有吸引力的特性或解释。

图像矩对于分割之后对象的描述是有用的。通过图像矩得到的图像的简单属性包括面积（或总强度），其质心和关于其方向的信息。

原点矩
对一个二维连续函数 $f(x,y)$ ，第 $(p+q)$ 个点的矩（原点矩）被定义为
$M_{pq} = \int\limits_{-\infty}^{\infty} \int\limits_{-\infty}^{\infty} x^p y^q \,f(x,y) \,dx \,dy \quad \quad p,q=0,1,2,...$
照这个思路，像素强度为 $I(x,y)$ 的灰度图，原点矩为：
$M_{ij}=\sum\limits_x \sum\limits_y x^i y^i I(x,y)$
有些情况下，也可以把图像看成概率密度函数来计算 $\sum\limits_x \sum\limits_y x^i y^i I(x,y)$

唯一性定理(Hu[1962])指出，如果 $f(x,y)$ 是分段连续的并且仅在xy平面的有限部分中具有非零值，则存在所有阶的矩，并且矩序列 $M_{pq}$ 由 $f(x,y)$ 唯一确定。
反之，中心矩 $M_{pq}$ 唯一确定 $f(x,y)$ 。
在实践中，图像被概括为具有几个较低阶矩的函数。
举个栗子，Opencv中moment函数从原点矩中获得的简单图像属性
面积（二值图）或灰度和（灰度图）：M00
质心： ${\bar{x},\bar{y}}={ \frac{M10}{M00},\frac{M01}{M00} }$

  vector<Moments> mu(contours.size() );
 vector<Point2f> mc(contours.size() );
 mu[c] = moments( contours[i], false );
 double area=mu[c].m00 ;
 mc[c] = Point2f( mu[c].m10/mu[c].m00 , mu[c].m01/mu[c].m00 );

中心矩

中心矩被定义为： $\mu_{pq}=\int\limits_{-\infty}^{\infty} \int\limits_{-\infty}^{\infty} (x-\bar{x})^p (y-\bar{y})^q \,f(x,y) \,dx\,dy \quad \bar{x}=\frac{M_{10}}{M_{00}} ,\bar{y}=\frac{M_{01}}{M_{00}}$

如果是数字图像，则等式变为：

$\mu_{pq}=\sum\limits_x \sum\limits_y (x-\bar{x})^p (y-\bar{y})^q\,f(x,y)$

3阶及以下中心矩依次为：

$\mu_{00}=M_{00},\\ \mu_{01}=0,\\\mu_{10}=0,\\ \mu_{11}=M_{11}-\bar{x}M_{01}=M_{11}-\bar{y}M_{10},\\ \mu_{20}=M_{20}-\bar{x}M_{10},\\ \mu_{02}=M_{02}-\bar{y}M_{01},\\ \mu_{21}=M_{21}-2\bar{x}M_{11}-\bar{y}M_{20}+2\bar{x}^2M_{01},\\ \mu_{12}=M_{12}-2\bar{y}M_{11}-\bar{x}M_{02}+2\bar{y}^2M_{10},\\ \mu_{30}=M_{30}-3\bar{x}M_{20}+2\bar{x}^2M_{10},\\ \mu_{03}=M_{03}-3\bar{y}M_{02}+2\bar{y}^2M_{01},$

总结出来就是

$\mu_{pq}=\sum\limits_x \sum\limits_y \left( \begin{array}{c} p\\m \end{array} \right) \left( \begin{array}{c} q\\n \end{array} \right) (-\bar{x})^{p-m} (-\bar{y})^{q-n} M_{mn}$

中心矩具有平移不变性

举个栗子
图像方向的信息可以通过首先使用二阶中心矩来构造协方差矩阵导出(底下这个式子很明显就是矩阵降维)

$\mu'_{20}=\frac{\mu_{20}}{\mu_{00}}=\frac{M_{20}}{M_{00}}-\bar{x}^2 \\ \mu'_{02}=\frac{\mu_{02}}{\mu_{00}}=\frac{M_{02}}{M_{00}}-\bar{y}^2 \\ \mu'_{11}=\frac{\mu_{11}}{\mu_{00}}=\frac{M_{11}}{M_{00}}-\bar{x}\bar{y}$

其中，图像上一点 $I(x,y)$ 的协方差矩阵为

$cov[I(x,y)]=\begin{bmatrix} \mu'_{20} & \mu'_{11} \\ \mu'_{11} & \mu'_{02} \end{bmatrix}$

矩阵的特征向量对应于图像强度的长轴和短轴，因此可以从与最大特征值相关联的特征向量的角度朝向最靠近该特征向量的轴提取取向。可以证明，该角度 $θ$ 可由以下公式得出：

$\Theta=\frac{1}{2}arctan\bigg( \frac{2\mu'_{11}}{\mu'_{20}-mu'_{02}} \bigg) \quad \mu'_{20}- \mu'_{02} \neq 0$

协方差矩阵的特征值可以表示为：

$\lambda_i = \frac{\mu'_{20}+\mu'_{02}}{2} \pm \sqrt{\frac{4\mu '_{11}+(\mu '_{20}-\mu '_{02})^2}{2}}$

且特征值与特征向量轴的长度的平方成比例。特征值的幅度的相对差异体现了图像的偏心特性或者说他多细长。偏心率是：

$\sqrt{1-\frac{\lambda_2}{\lambda_1}}$

矩不变性

矩因为其在图像分析上的应用广为人知，由于他们可以被用于导出关于特定变换类的不变量。，

在这种情况下，不变矩这个术语常被滥用。然而，虽然矩不变量是从矩中形成的不变量，不变量本身的唯一矩是中心矩。

注意下面的详细的不变量仅在连续区间保持不变性。在离散区间，尺度和旋转都不能很好的形成，离散图像转换是近似的，且变换不可拟。因此，当描述离散图像中的形状时，这些不变量仅是近似不变的。

平移不变性
通过构造，任意阶中心矩$\mu_{ij}相对于平移都是不变的。

尺度不变性
相对平移和尺度的不变量ηijηij可以通过适当的缩放零阶中心矩阵从中心矩构建

$\eta_{ij}=\frac{\mu_{ij}}{\mu_{00}^{1+\frac{i+j}{2}} } \quad i+j \geq 2 \\$

注意平移不变量仅仅在中心矩时直接跟随使用。

旋转不变性
正如Hu等人的工作所示，可以构建关于平移、放缩和旋转的不变量:

$I1=\eta_{20}+\eta_{02} \\ I2=(\eta_{20}−\eta_{02})^2+4\eta_{11}^2 \\ I3=(\eta_{30}−3\eta_{12})^2+(3\eta_{21}−\eta_{03})^2 \\ I4=(\eta_{30}+\eta_{12})^2+(\eta_{21}+\eta_{03})^2 \\ I5=(\eta_{30}−3\eta_{12})(\eta_{30}+\eta_{12})[(\eta_{30}+\eta_{12})^2−3(\eta_{21}+\eta_{03})^2]+(3\eta_{21}−\eta_{03})(\eta_{21}+\eta_{03})[3(\eta_{30}+\eta_{12})^2−(\eta_{21}+\eta_{03})^2] \\ I6=(\eta_{20}−\eta_{02})[(\eta_{30}+\eta_{12})^2−(\eta_{21}+\eta_{03})^2]+4\eta_{11}(\eta_{30}+\eta_{12})(\eta_{21}+\eta_{03}) \\ I7=(3\eta_{21}−\eta_{03})(\eta_{30}+\eta_{12})[(\eta_{30}+\eta_{12})^2−3(\eta_{21}+\eta_{03})^2]−(\eta_{30}−3\eta_{12})(\eta_{21}+\eta_{03})[3(\eta_{30}+\eta_{12})^2−(\eta_{21}+\eta_{03})^2].$

这就是众所周知的HU矩不变量。

第一个，I1,类似于围绕图像的质心的转动惯量，像素强度类似于物理密度。
最后一个，I7,倾斜不变性，有能力区分其他相同图像的镜像。(不懂)

J. Flusser提出了推导完整和独立的旋转矩不变量集合的一般理论。他所传统的Hu矩既不独立也不完全。I3并不是非常有用，因为他不独立，依赖于其他不变量。原始的Hu集合中有一个缺失的三阶独立不变矩。

$I8=\eta_{11}[(\eta_{30}+\eta_{12})^2−(\eta_{03}+\eta_{21})^2]−(\eta_{20}−\eta_{02})(\eta_{30}+\eta_{12})(\eta_{03}+η21)$

后来，J.Flusser和T.Suk就专门研究N旋转对称形状的情况。

点云意义

PCL点云库关于矩的使用有两个，一个是pcl::MomentInvariantsEstimation,估计每个3D点处的三个矩不变量(j1,j2,j3)。另一个就是 pcl::MomentOfInertiaEstimation 类。可以获得基于偏心率和转动惯量的描述符。还能提取点云的对齐轴和定向边界框。

Note:提取的边界框不是最小可能的边界框。

先讲特征提取的idea。首先计算点云的协方差矩阵，并提取其特征值和向量。你也可以想象成归一化合成的特征向量，且总是形成右手坐标系（主特征向量表示x轴，次向量表示z轴）。下一步执行迭代。每次迭代过程中，主特征向量旋转。旋转顺序不变，且围绕其他特征向量执行。这提供了点云的旋转不变性。因此，我们把这个旋转的主矢量当成当前轴。

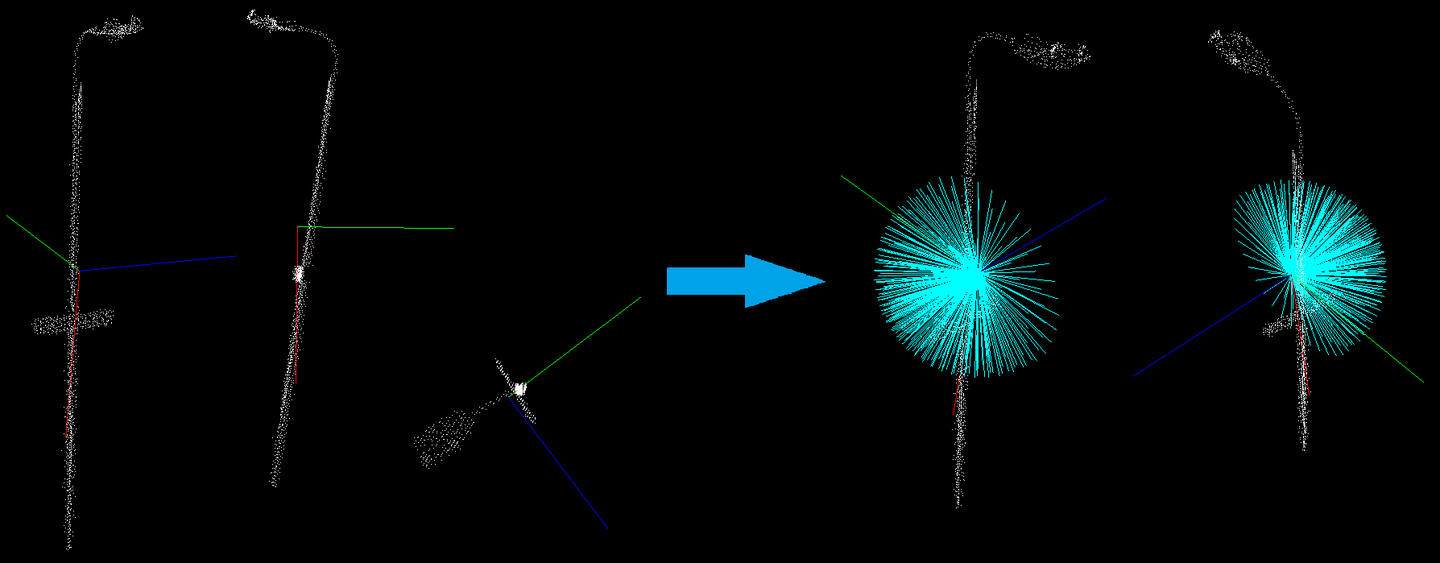
对于每个当前轴，计算转动惯量。另外，当前轴已被用来计算偏心率。因此，当前向量被看成平面法向量，并且将输入的点云投影到他上面。根据所获得的投影计算偏心率。

当然，这个类还提供了获取Axis Aligned Bounding Box(AABB)和Oriented bounding box(OBB)的接口。将AABB作为特征向量计算OBB。pcl提供了一个[示例](http://pointclouds.org/documentation/tutorials/moment_of_inertia.php)，来体会矩的计算。

参考：

zh.wiki/矩（数学）

wiki/moments(math)

wiki/moments(physics)

偏度和峰度如何影响您的分布

wiki/Image_moment

pcl/tutorial/moment_of_inertia

CVonline_moments

编辑于 2018-04-08

因为我们常常会将随机变量（先假定有任意阶矩）作一个线性变换，把一阶矩（期望）归零，二阶矩（方差）归一，以便统一研究一些问题。这时候，在同样期望为0方差为1的标准情况下（以下均假设随机变量满足该条件），随机变量最重要的指标就变成了接下来的两个矩了。
三阶矩，就是我们所称的「偏度」。粗略来说，一个典型的正偏度变量X的分布满足这样的特征：很大的概率X会取绝对值较小的负值，但在极少数情况下，X会取特别大的正值。可以理解为「一般为负，极端值为正」。典型的正偏度投资，就是彩票和保险：一般来说，你花的那一点小钱就打水漂了，但是这一点钱完全是在承受范围内的；而这点钱则部分转化为小概率情况下的巨大收益。而负偏度变量则正好相反，「一般为正，极端值为负」，可以参照一些所谓的「灰色产业」：一般情况下是可以赚到一点钱的，但是有较小的概率「东窗事发」，赔得血本无归。
四阶矩，又称峰度，简单来说相当于「方差的方差」，和偏度类似，都可以衡量极端值的情况。峰度较大通常意味着极端值较常出现，峰度较小通常意味着极端值即使出现了也不会「太极端」。峰度是大还是小通常与3（即正态分布的峰度）相比较。
至于为什么五阶以上的矩没有专门的称呼，主要是因为我们习惯的线性变换，只有两个自由度，故最多只能将前两阶矩给「标准化」。这样，标准化以后，第三、第四阶的矩就比较重要了，前者衡量正负，后者衡量偏离程度，与均值、方差的关系类似。换句话说，假如我们能把前四阶矩都给「标准化」了，那么五阶、六阶的矩就会比较重要了吧。
-
我曾经和
讨论过类似的问题。要是把一个人的一生当作一个函数f(t)（t是时间），那么「一阶矩」（整个人生的积分，即∫f(t)dt）就可以用来衡量这一生总体是好还是坏；而「二阶矩」（整个人生的平方积分，即∫[f(t)]^2dt，下同）则衡量这一生是一帆风顺还是大起大落。
然而，正所谓「久入芝兰之室而不闻其香，久入鲍鱼之肆而不闻其臭」。生活条件优越（一阶矩较正）的人，已经习惯了，于是一点点不顺心也会当作大事；生活风平浪静（二阶矩较小）的人，则一点点起落也会表现得很敏感。于是，我假定每个人对自己人生的主观感觉g(t)，就是对f(t)做了一个线性变换以将一、二阶矩都标准化。这么看来，其实每个人的人生都差不多，一阶矩都是0，二阶矩都是1。
但是真的是如此吗？后来我自己思考了一下，将一、二阶矩都标准化后，下一个显著特征就是三阶矩（∫[g(t)]^3dt）了。前面提到，三阶矩比较正的，就是「一般负，极端正」。三阶矩很正的人生，多为那些暴发户，庸碌终生，显赫一时；而是三阶矩很负的，「一般正，极端负」，则可以参照那些「温室的花朵」，平时很优越，但一次挫折就迅速毁了这个人的一生。所以不同的人生还是不一样的吧。
-
2017-2-4补充：四阶矩（∫[g(t)]^4dt）远小于3的人生，是比较常规的，有欢笑，也有泪水，不会有什么太大的变动，偶尔的大悲大喜也未尝不是一份宝贵的经历。而四阶矩远大于3的人生，则会明显地有那么几次大起大落，它们对你的影响是如此深刻，以致于面对生命中其他的欢笑和泪水时，总是麻木地、带着苦笑地一笔带过了，丝毫无法在内心激起哪怕一丝波澜；当回首一生，除了那么几个时间节点，几乎没有任何可圈可点的内容。这么看来，不同的人生就更不一样了。
-
2017-4-5补充：再提供一个理解的角度，有错误的话请指正：
集中收益，分散风险：正偏度
分散收益，集中风险：负偏度
集中收益，集中风险：大峰度
分散收益，分散风险：小峰度

编辑于 2017-04-05

如何理解概率论中的“矩”？

给我一个支点和一根足够长的棍子，我就可以举起整个地球。

----阿基米德

对比物理的力矩，你会发现，概率论中的“矩”真的是很有启发性的一个词。

1 力矩

大家应该都知道物理中的力矩，我这里也不展开说细节了，用一幅图来帮助大家回忆一下：

上图中，两边能保持平衡，只要满足下面的式子就可以了（很粗糙的式子，没把力作为向量来考虑）：

$F_1D_1=F_2D_2$

其中， $F_1D_1,F_2D_2$ 都称为力矩。

可以看出上图的 $F_1$ 大， $F_2$ 小，但由于杆子长度不同，仍然可以取得平衡。

利用上图的原理，我们就可以制作出秤：

2 概率论中的“矩”

在概率论中，有一杆无处不在的“秤”。因为这把“秤”的存在，所以我们有了“矩”。

2.1 彩票的问题

福利彩票，每一注两元钱，真是中国的良心啊，猪肉、房价都涨了多少了！？

每一注的中奖几率如下（胡诌的）：

画成概率分布大概就是这样的：

不过，我想你大致不会认为，这花两元钱买的彩票，真的就价值五百万。

我们用概率来组装一把“秤”：

“秤”摆好了，我们尝试称一下：

称量实际上是：

这么少？不是说好了五百万的吗？

没有办法，中奖概率太低了，离秤的中心太近了（对应于力矩而言，就是力臂太短了）。中国有句古话：“二鸟在林不如一鸟在手”，说的真的有道理啊。

把整张彩票都放上去称（秤上的刻度是随便画的，因为相差太悬殊，没有办法按照真是比例来画）：

具体计算如下：

$1.5=5\times10\%+100\times0.5\%+5000000\times0.00001\%$

这张彩票原来只值1.5元？血本无归啊！

3 “矩”

学过概率的都知道，我们上面计算的就是期望：

$\displaystyle E[X]=\sum_{i}p_{i}x_{i}$

其实这就是“矩”：

因为 $x$ 是一次幂，所以也称为“一阶矩”。

再比如方差：

$\displaystyle Var(X)=E\left[(X-\mu)^2\right]=\sum_{i}p_{i}(x_{i}-\mu)^2$

其中的距离 $(X-\mu)^2$ 也需要称量之后才能使用，所以方差也称为“二阶矩”。

“三阶矩”、“四阶矩”、“高阶矩”，各有用途，但是共同的特点就是称量之后才能使用。

Road to Analyst

Thursday, March 5, 2020

Moment 矩

更多回答