导读
1、作为西学东渐--海外文献推荐系列报告第六十五篇,本文推荐了Grinblatt M,和Saxena K.于2018年发表的论文《Improving Factor Models》。
2、传统的alpha因子挖掘往往以FF3因子,Carhart4因子,FF5因子等因子模型为基准,来说明其相对这些基准模型有额外的alpha。作者对这些基准模型提出了质疑,是否是这些基准模型的构造方式导致了其定价能力的不足?
3、本文从Ross的无套利定价理论(APT)出发,指出传统的因子定价模型中,因子收益往往通过单个因子分组后两端组合的等权收益之差来代表,这种构造方式是因子定价模型无法解释众多因子异象的关键原因。作者提出了一种新的方法:使用多个因子的分组组合,并且通过最大化夏普比率给每个组合若干权重,来构造一个新的单因子基准组合。在这种基准模型下,10个著名的因子异象都不再显著。
4、作者的这种将多个因子的组合通过夏普最大化构造一个组合的方式,不仅对于因子定价模型有贡献,对我们实务中检验与构造新的因子,构造量化策略均有一定的指导意义。
风险提示:文献中的结果均由相应作者通过历史数据统计、建模和测算完成,在政策、市场环境发生变化时模型存在失效的风险。
1、引言
Ross虽然不是因子模型的奠基人,但是他首先将因子模型的风险与个股的预期收益进行了结合。1976年Ross研究的核心是构造一个充分分散的股票组合,去模拟因子的收益,非因子来源的收益对组合干扰很小,因为这些收益干扰很容易通过分散化避免。在这种“没有意外干扰”的假设下Ross的资产定价理论才能够成立,因此才有了简洁优美的数学表达:当风险的维度(因子个数)相对资产个数很少时,资产的超额收益完全由其在因子上的暴露所决定。即在无套利的假设下,无套利定价理论(APT)可以被表达为优美的线性等式。
Ross的APT理论虽然很优美但其在现实中却不成立:至今有数百个因子异象存在(因子异象指的是在因子定价模型外存在能够显著预测股票收益的因子的现象)。这些异象不能被一些纯统计方法如PCA所解释,也不能被基于宏观冲击的因子模型所分解。我们不知道为什么APT无法解释这些异象,但Kandel [1985]、Grinblatt和 Titman [1988]的研究提出了一种猜想:他们把这些因子异象视为因子定价模型的基础。
这几十年来,因子异象越来越流行,也被越来越多人所接受:自FF3因子模型提出以来,这种以某个资产特征(如市值、市净率)构造两个极端的资产组合,进而构造因子的方法逐步替代了之前纯统计方法或者基于宏观冲击的因子构造方法。截止到20世纪90年代,这种基于资产特征的因子构造方法已经非常普及,然而这些因子都是各自独立的风险来源。学者们都是基于超额收益而非风险角度把这些因子挖掘出来,但APT理论告诉我们每个因子都有其对应的风险。
在某种程度上,这种基于超额收益的因子构造方式的效果很好。比如Fama 和French [1992]在研究中发现CAPM模型无法解释成长股与价值股之间的收益差别:这种现象违背了Ross的APT模型,因此他们开发了HML(市净率)因子。但这些基于资产特征的模型往往无法解释其他特征因子的超额收益,如HML因子无法解释市值因子的超额收益。WML(Carhart[1997]提出的动量因子)可以解释高低动量股票的收益差,却无法解释成长因子,利润因子的收益差。不幸的是,当因子异象在增长的同时,(定价模型里的)因子数量也在相应的增长:至今已经有十多个定价模型中的因子都来自于这些因子异象。这违背了Ross APT模型的本意:用少数几个因子进行资产定价。仿照Grinblatt 和Saxena [2018]的方法,我们提供了一个思路,可以解释为什么少数几个基于资产特征的因子无法解释另一些基于资产特征的因子的收益,关键在于等权的多空组合。如HML因子收益是这样计算的:大市值低市净率的组合收益减去大市值高市净率的组合收益,再加上小市值低市净率的组合收益减去小市值高市净率的组合收益,这些组合都是基于市值和市净率极端分位数所划分的,且这四个组合的权重都是0.5或者-0.5。如果HML因子收益的定义方式稍作改变:将小市值的两个组合,高市净率的两个组合权重都增加一些, HML因子的收益将会不显著。
Grinblatt 和Saxena [2018]指出的一种基于预期收益(即最大化夏普)为组合配置权重的方法很有价值。这种方法会最大化组合的夏普比率,所以我们将其称为均值方差效率(MVE)因子组合。这种方法可以很好的解释大量因子异象。这篇文章介绍了这种方法,讨论了他的不足并对其做了简化。
2、主要方法:对因子组合进行权重分配
Grinblatt 和Saxena [2018]的研究一开始以四个因子异象下的各自5×5组合开始,共有100个组合,都是等权的。每个都是按照市值和特定因子进行分位数分组。四个因子来自于Carhart [1997] 、Fama 和French [2015]的研究,分别是市净率因子、投资因子,利润因子和动量因子(book-to-market ratio,investment, profitability, 和momentum)。这100个组合中,每个组合平均的股票数大于100,说明其充分分散,某一公司特质风险不会对组合产生很大影响。按照Ross的模型,有100只股票的组合,其特质风险的平均值是1%左右,可以说基本没有特质风险。
图表1的Panel A展示了这100个组合以及计算因子收益时这些组合的权重是如何配置的。如果股票的超额收益与其在因子中的暴露成比例,那么这个因子的定价能力就会比较好。Panel A把100个组合中的68个都涂成了灰色,代表其在计算因子收益时没有权重。这些零权重组合包括所有在中间格子里的组合以及5×5分组里的中间三行,这种做法背后的意思是大多数的超额都发生在两端。100个格子中共有32个白色格子,他们对应组合的月度(或更高频的)收益决定了其权重。通过最大化夏普,得到组合权重,再基于这些组合权重计算的收益就是我们构造的“单因子”的基准收益。最大化夏普作为一种金融研究领域通用的方法,计算时只需要这32个组合的平均收益与协方差矩阵。这种方法保证了所有的白色格子里的组合相对这个新基准没有alpha超额收益。
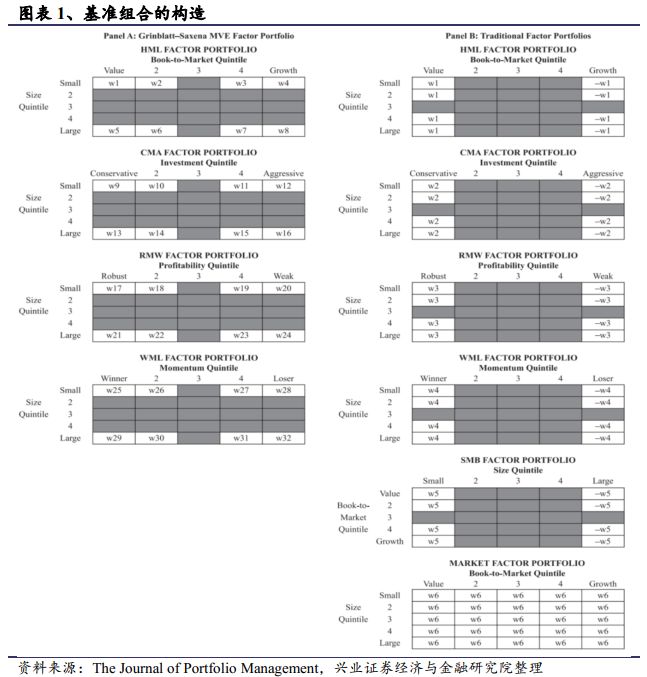
所有的多因子模型都可以生成一个类似的单因子基准组合。这种将传统的多因子组合基准转换为单因子基准的加权方法类似于Grinblatt 和Saxena [2018]的方法。与其主要的不同在于他们的方法还带有传统方法下的一系列约束。这些约束包括:如图表1的Panel B,所有的非零组合的权重绝对值相同。第一个矩阵中,左边的白色格子是一样的正负号,右边的白格子里是相反的正负号。约束权重w为了让组合的夏普最大化。大多数传统的因子模型还包含市场因子,即将所有格子赋予权重的矩阵。
更精确的讲,市场因子的矩阵各个格子的权重可以不等,它们的权重可以等比例于格子里组合的市值。传统的基准也有一些是2×3分组的,但这也与图表1展示的很类似。图表1只是想说明我们的方法与传统方法在权重配置方面的约束是不同的。至于图表1 Panel B的更多更精确的构造方法,与本文无关。
3、实证:解释10种著名的因子异象
如果因子的alpha收益在我们的单因子新基准下比传统的基准更低,Grinblatt 和Saxena [2018]关于单因子新基准的构造方法就是有效的。当alpha足够低时,则说明其因子异象不存在。图表2中,使用了1973年7月到2014年12月的数据,列示了10个著名的因子异象的收益,分别基于四种不同的传统因子模型基准,和三个版本的Grinblatt 和Saxena [2018]的MVE模型因子基准。他们分别是FF3因子模型,Carhart模型,FF5因子模型,以及FF6因子模型(用到了前面所有6个因子)。FF3因子模型由Fama 和French [1993]提出,三个因子分别是市场因子MKT,价值因子HML,市值因子SMB。Carhart四因子模型加入了动量因子WML。FF5因子,Fama 和French [2015]在FF3的基础上加入了投资因子和利润因子。FF6因子在FF5因子的基础上加入了动量因子WML。
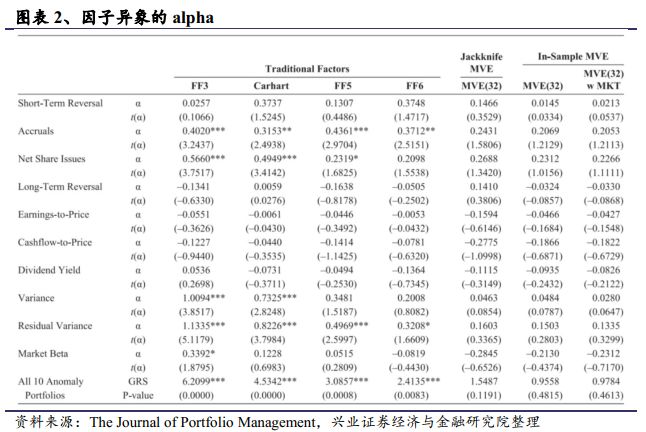
基于Grinblatt 和Saxena [2018]三个版本的模型通过调节32个子组合的权重,使最终构造的组合夏普最大化。这三个版本包括折叠版本(jackknife version),其权重都是基于不包括当期样本的所有数据计算的。比如对于2005年7月,使用1973年至2014年的除2005年7月的所有月度数据。折叠版本的权重接近于基于所有样本数据的权重。折叠版本的最优权重每个月都会变化。因此,折叠版本的测试是样本外的测试。除了其不会剔除本月的数据,样本内的MVE版本做法与折叠版本完全相同。因此,每个月样本内的MVE版本在32个组合的权重是相同的。带有MKT因子的样本外MVE模型就是将MKT因子加入到基准之中。
折叠版本模型的样本外方法避免了样本内最大化的统计偏差,然而这种偏差在样本数量很大的时候可以忽略不计。图表2展示了两个版本的基准比较,10个异象中有9个:因子异象在折叠版本的alpha大于样本内MVE版本的alpha,但二者之差非常小,F统计量显示这10个alpha都不显著。
4、关于模型的细节探讨
4.1
传统模型与MVE模型下的因子异象的alpha
图表2的关键信息是相比传统的基准,在3个MVE基准下,因子的alpha与0非常接近。没有一个异象能够在10%的显著性水平下显著非0。另外,折叠版本MVE基准下的因子alpha要比样本内版本MVE基准下alpha更大一些,但它们在Gibbons, Ross, 和Shanken [1989](GRS)的F统计量下依然是不显著的。GRS的F统计量的P值都大于0.1,所有的10个异象的alpha在统计上都不显著。而在传统模型下,几个alpha仍然是显著的,且他们的p值都小于0.01,说明在传统模型下这四个因子的alpha在1%显著性水平下显著。
在传统模型的基准下,FF6模型尽管存在显著的F统计量,但它很好的解释了异象,只有3个因子的alpha超过了30bp每月,只有2个因子的alpha在10%水平下显著。然而,三个MVE基准下没有因子的alpha超过30bp每月,没有因子的alpha在10%的显著性水平下显著。这里说明一点,FF6模型并不是一个通用的传统模型,他实际上是我们基于FF3因子,Carhart4因子,和FF5因子模型融合的因子模型。
4.2
应该用多少数据
图表2用了整个数据样本检验不同构造方法的区别,但因子异象的收益均值,方差,协方差可能会随时间变化。对于时变的均值方差与协方差,构造基准组合与估计因子系数的时间窗口长度应该缩短。这是因为在最大化夏普的目标下,基础组合当前真正的最优权重相对于用很长时间窗口计算的最优权重,会偏离很多。对基准组合较差的参数估计会造成因子异象alpha显著。
统计学有一条规律:当一个数据生成过程的参数变化缓慢或者不变,样本越多参数估计越准确。因为较长的样本期可以消除更多的随机扰动。这些随机扰动可能会造成样本的统计量偏离其真值,所以根据最大化夏普计算的参数也会因随机扰动偏离其真值。更长的样本期可以更准确地估计因子的beta与alpha。
图表3与图表2的相同之处是比较了4个传统模型与3个MVE模型,不同之处是MVE模型使用滚动的样本期长度。图表3的Panel A使用240个月进行基准权重的估计,Panel B到D分别用180,120,60个月。这些Panel中的alpha,t统计量,F统计量,P值都是在各自窗口期下的平均值。比方说,Panel A的第一个观测值是基于样本1-240(第1期到第240期)计算的,第二个第三个观测值是基于样本2-241,3-242计算的。最终我们把每期得到的结果进行平均。
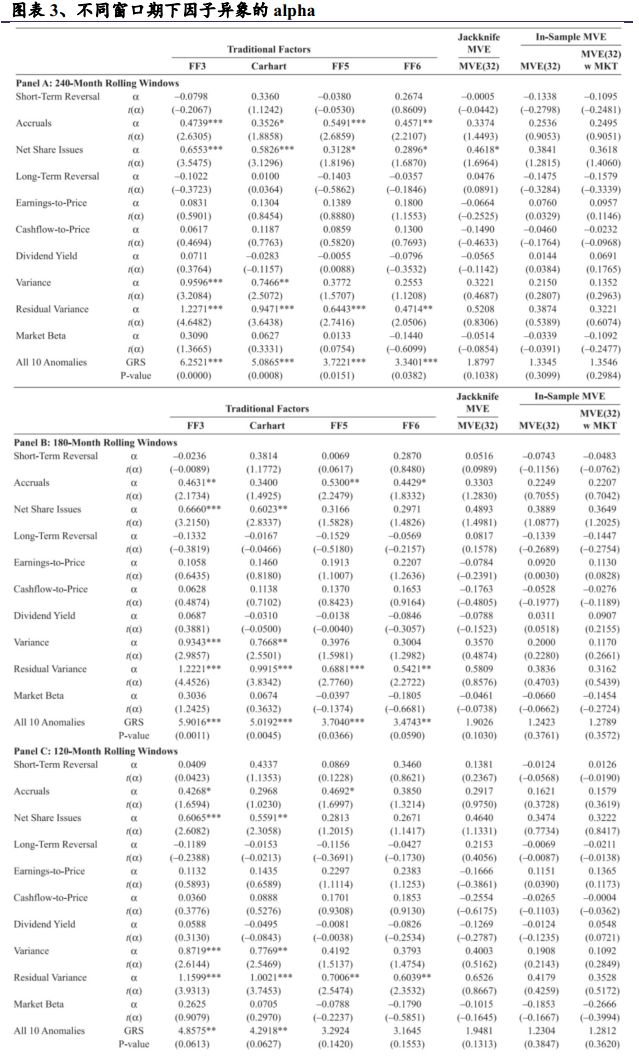
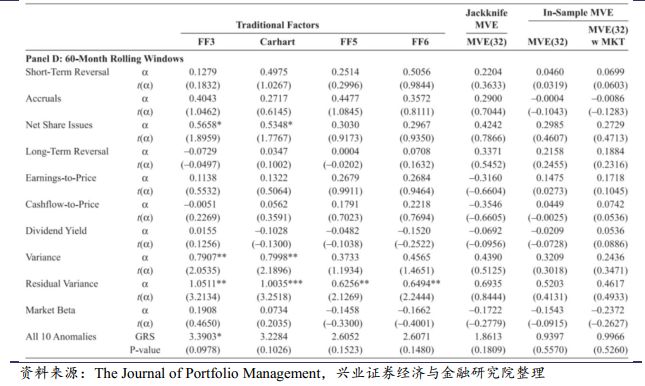
图表3得到的结论与图表2大致相同。例如,对所有的Panel,加入市场因子的影响都很小,对于最后一行的P值,折叠版本的模型比其他传统模型都要高,说明其解释因子异象的能力要比传统模型更好。另一方面,较短的时间窗口如120, 60个月(Panel C 和D),折叠版本模型的P值要更接近于FF6模型的P值。这说明参数估计中的噪声一定程度上降低了MVE模型的资产定价能力。但与图表2相同的是,图表3中MVE模型下的P值都大于0.1。
4.3
样本内版本与折叠版本MVE模型
样本内版本的MVE模型估计的alpha,t统计量,F统计量都不显著。真实的P值应该落在折叠版本下的P值与样本内版本的P值中间。这两种版本下的alpha很接近(如图表2,图表3的Panel A B)且都很接近于0。对于240个月的折叠版本与样本内版本,二者的权重估计差别来自于240个样本中的1个样本,这1个样本所造成的偏差忽略不计。既然如此我们相信样本内MVE模型的P值等统计量与真实值非常接近。因此对于15年(180个月)以上的样本数量来说,使用样本内MVE模型进行异象的判别没有什么问题,且这种模型相对更简洁,计算复杂度更低,更能成功的解释因子异象。
当样本期数量(即时间窗口长度)是120,60个月(Panel C D)时,折叠版本与样本内版本的因子异象alpha相差的更多一些。这说明样本内MVE版本的结果更好是因为其过拟合。图表4展示了Panel A到E的alpha相关性,不同样本期的模型展现了一定差异。Panel D中10个异象的平均相关性低于0.8,而Panel E中的平均相关性则大于0.9,比其他Panel的相关性都要高。所以,只有当样本长度大于15年,样本内MVE模型在因子异象的检验上才可以替代折叠模型。
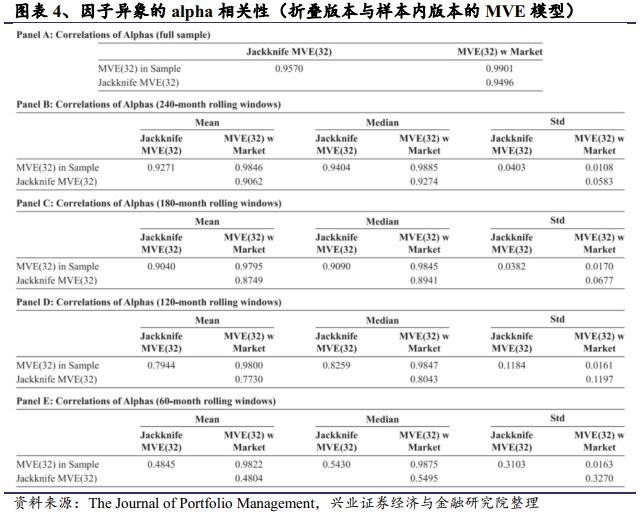
在更短期的MVE模型中,检验的结果可能源自于挖掘样本内的统计偏差。当样本区间长度与实际因子收益生成的区间长度相差较大时,这种样本期长度下的基准就远不是最好的。如果要将MVE模型运用到较短的样本期长度,折叠版本的模型是一个更可靠的选择。
4.4
市场因子的收益对因子定价有帮助吗?
图表2,3,4显示,是否加入市场因子对于模型检验的alpha几乎没有影响,市场因子并不能提升组合的解释与定价能力。实际上,是否加入市场因子对于因子异象alpha的影响是1到2bp每月。图表4加入市场因子与不加入市场因子的模型下alpha相关性分别是0.98与0.99。图表2,3中的F统计量与P统计量,在市场因子加入前后也基本相同。因此,市场因子对于MVE模型的作用类似于人类的尾椎,它曾经是资产定价模型进化过程中的重要角色,但现在几乎没用了。
前文中的10个异象因子包括了价值,动量,投资因子,原因是它们本身就是构造基准组合的因子。把它们加入检验是比较合理的。
4.5
模型能否解释因子组合的alpha?
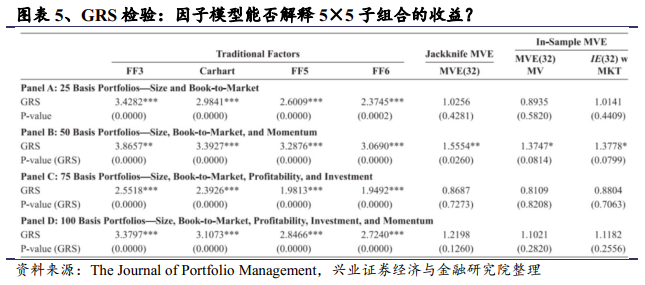
为了比较模型对不同的因子集所构造组合的alpha的检验能力,我们在图表5的Panel A到D中列示了4种因子组合(每个组合都用到了不同传统模型中的因子)。他们分别具有25个,50个,75个和100个子组合,图表5展示了他们各自的F统计量。F统计量检验的是他们这四个子组合构造的组合收益alpha是否显著,结果显示,每种子组合的情况下,传统模型下这些alpha都是显著的,但MVE模型基准下这些子组合的alpha都不显著。
4.6
市场因子的运用对MVE模型的影响
图表2 3中是否带有市场因子,对于样本内MVE模型检验的alpha来说差别很小,图表5中两个模型的alpha相关性分别是0.945与0.953。是否加入市场因子对于alpha检验的影响很小。且加入了市场因子后, P值变得稍小,说明不加市场因子的MVE模型定价能力稍好,但我们的模型的定价能力无论是否加入市场因子都很强。
4.7
多少个子组合应该限制为0权重
至今为止,我们看到了MVE组合能够更好的解释因子及因子组合的超额收益。对于样本期长度在15年以上的样本内及折叠版本的模型,他们得到的alpha与t统计量十分接近。MVE模型与传统定价模型的本质区别是MVE模型更加注重均值方差的实现效率。传统模型对于非零权重的子组合赋予同样的权重绝对值,而MVE模型则是以最大化夏普为目标分配子组合的权重。对子组合的权重限制(传统模型使这些权重的绝对值都相等)是这两种模型定价差异的主要原因。
MVE模型基准也带有传统模型基准的一些限制,即让一些子组合权重限制为0。为什么我们不把这些限制也拿掉呢?比如,对于市值和市净率因子的25个子组合,我们可以将它们用一定权重结合起来,构造一个MVE基准。这样构造的单因子组合肯定会很好的解释掉这25个子组合的收益。然而这种方法有数据挖掘的嫌疑,这样构造的单因子组合基准很难对除这25个子组合以外的组合进行定价。换句话说,样本内的过度优化过程让单因子组合基准的定价能力大打折扣。
图表6的Panel A展示了MVE(100)基准,展示了允许100个组合的权重都不为0的情况下的定价能力。Panel B C分别展示了允许64个,16个组合权重不为0的模型。他们分别统计了图3中3个时间窗口(240,180,120个月)下的F统计量与P统计量均值。图表6的Panel A B分别是MVE(100),MVE(64),比我们之前用到的MVE(32)模型中,被约束为0的子组合要少,他们折叠版本基准的F统计量在5%的显著性水平下显著。因此,放松MVE(32)模型中关于子组合0权重的限制,会有些过拟合,他们的最优化得到的权重,与真实值相差更远。尽管所有的样本内MVE组合下,关于因子异象的统计量都是不显著的,这种现象主要因为样本内的过度拟合,也就是说MVE(100),MVE(64)模型的过拟合风险会更大一些。相比之下,MVE(16)的样本内和折叠版本模型得到的结论与MVE(32)类似,说明只需要把大多数子组合的权重限制为0即可得到一个较好的定价模型。
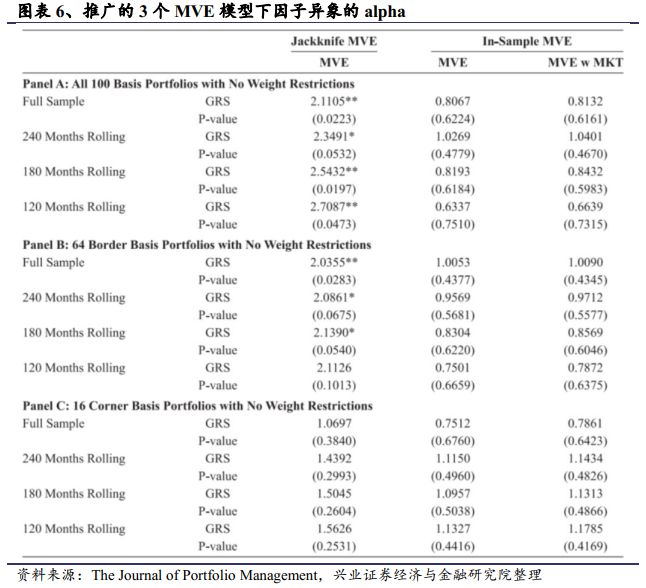
总的来说,虽然样本内MVE模型在很多情况下,尤其是样本期很长,子组合自由度低的情况下,都是一个较为方便简单的模型,但只有当折叠版本的MVE模型检验的alpha与样本内MVE模型相差不多时,结论才是比较可靠的。保守的讲,只有将所有的内部子组合权重都限制为0的时候,用我们方法构造的模型的定价能力才比传统定价模型的高。
5、结论
提升因子模型的定价能力与其说是科学,更像是一种艺术。因为我们无法观察到真正的均值方差协方差,所以让构造的基准组合夏普最大化是一项艰难的工作,我们只能通过样本的均值方差协方差来进行替代。尽管如此,Ross的APT理论可以给我们一些指导。
APT理论告诉我们,可以构造充分分散的资产组合,使其仅与特定因子的beta有关,与其他因子线性无关,因为有这些组合,我们才有可能构造一个合适的基准。然而,我们不知道因子的数量和名称,所以找到这些线性无关的beta因子是几乎不可能的工作,尤其当这些因子数很大的时候,这种工作甚至无法实现。金融领域的研究人员对这种情况的解决方式是在一个较少因子数量的定价模型基础上挖掘更多定价因子,因子多空组合的收益是挖掘新因子的标准方法。
定价因子对于资产定价来说非常重要,非定价因子却与资产定价无关,使用一些统计方法如PCA,因子分析,无法区分定价因子与非定价因子的重要性。然而,APT模型告诉我们:可以构造一系列组合,这些组合只与某个因子有关,而与其他因子正交。我们用MVE方法实现了这种组合的构建。过去的方法在构造定价模型时,忽略了样本的均值,方差和协方差。
我们提出的方法是使用样本的均值方差协方差来构造这种单因子组合基准。我们用它对10个因子异象与最多100个因子组合的收益进行了分解,证明了模型对于资产定价的能力。
我们的主要结论如下:第一,将分组的因子子组合中不在边缘的子组合权重限制为0,这样有助于最大化夏普过程的准确,避免了过度拟合。第二,加入市场因子并不能提高模型的定价能力。第三,我们的模型没有过度拟合,因为在15年以上的样本期内,折叠版本与样本内版本的结果十分接近。在较短的样本期,我们使用折叠版本的模型,没有用到当期的数据,模型的定价能力已然强于传统模型。第四,我们不能忽视样本的信息,MVE的优化方法对因子模型的定价能力十分有用。总的来说,单因子基准组合的设计中不能加入较多的限制,这样会影响其定价能力。传统计算因子收益的多空组合收益之差的方法,就是最极端的例子。一旦我们放松了这些限制,Ross的APT模型就可以解释更多的现象。
参考文献
【1】Carhart, M. 1997. “On Persistence in Mutual Fund Performance.” The Journal of Finance 52 (1): 57–82.
【2】Elton, E. J., and M. J. Gruber. 1973. “Estimating the Dependence Structure for Share Prices: Implications for Portfolio Selection.” Journal of Finance 28: 1203–1232.
【3】Fama, E. F., and K. R. French. 1992. “The Cross-Section of Expected Stock Returns.” The Journal of Finance 47: 427–465
【4】——. 1993. “Common Risk Factors in the Returns on Stocks and Bonds.” Journal of Financial Economics 33 (1): 3–56.
【5】——. 2015. “A Five-Factor Asset Pricing Model.” Journal of Financial Economics 116 (1): 1–22.
【6】Gibbons, M. R., S. A. Ross, and J. Shanken. 1989. “A Test of the Efficiency of a Given Portfolio.” Econometrica 57 (5):1121–1152.
【7】Grinblatt, M., and K. Saxena. 2018. “When Factors Don’t
Span Their Basis Portfolios.” Journal of Financial and Quantitative Analysis (forthcoming).
【8】Grinblatt, M., and S. Titman. “The Evaluation of Mutual Fund Performance: An Analysis of Monthly Returns.” Working paper, University of California, Los Angeles, 1988.
【9】Hou, K. R., C. Xue, and L. Zhang. 2015. “Digesting Anomalies: An Investment Approach.” Review of Financial Studies 28: 650–705.
【10】Huberman, G., and S. Kandel. “A Size Based Stock Returns Model.” Working paper, University of Chicago, 1985.
【11】Newey, W. K., and K. D. West. 1987. “A Simple, Positive Semi-Definite, Heteroskedasticity and Autocorrelation Consistent Covariance Matrix.” Econometrica 55: 703–708.
【12】Novy-Marx, R. 2013. “The Other Side of Value: The Gross Profitability Premium.” Journal of Financial Economics 108 (1): 1–28.
【13】Pastor, L., and R. F. Stambaugh. 2003. “Liquidity Risk and Expected Stock Returns.” Journal of Political Economy 111 (3): 642–685
【14】Ross, S. A. 1976. “The Arbitrage Theory of Capital Asset Pricing.” Journal of Economic Theory 111 (3): 341–360.
【15】Sharpe, W. F. 1963. “A Simplified Model for Portfolio Analysis.” Management Science 9 (2): 277–293
【16】Stambaugh, R., J. Yu, and Y. Yuan. 2012. “The Short of It: Investor Sentiment and Anomalies.” Journal of Financial Economics 104: 288–302.
风险提示:文献中的结果均由相应作者通过历史数据统计、建模和测算完成, 在政策、市场环境发生变化时模型存在失效的风险。